1965 Epiphone FT-79 Texan Scale Length

[Robbie Collins]

Does anyone have a measurement for the scale of a mid-60s Texan?

I'm about to slot the bridge the saddle and took a measurement from the nut to the middle of the 12th fret and got 12 & 11/16ths which, doubled, gives me 25-3/8". 

I looked to the Epi site. The copy about their "Inspired by Texan" reissue states the vintage Texan was based on the J-45 but with a 25.5" scale instead of 24.75.

25-3/8" isn't, by my thinking close enough to 25.5 to round up so, of course, it made me check my measurements. I used a 36" aluminum rule and a two tapes and got the same thing, measuring from the center of the nut to the center of the 12th fret and checking to make sure I was vertical, etc.

What do you use to measure scales? My 36"seems reasonably accurate but measuring and layout tools are something I don't want to economize on. Be great if there was a very accurate, stiff yardstick with a lip on one edge like a tape measure to measure the fretboard when the nut is off.

[Robbie Collins]

Do you mean you use something like StewMac's Fret Calculator to figure out the ideal distance from the nut for, say, the 21st fret and check the guitar against that?

[David Farmer]

Use any calculation for the distance from first to  the twenty-first. sometimes fretboards are short at the nut end.

 

[Ned Knepp]

Hi David,

 I'm afraid that I don't get it. When I figure a scale length, I usually start by verifying the actual fret spacing which can be fairly weird on some of the low end instruments I've seen. Once I'm sure that the nut -12th fret spacing is accurate, I double that to the bridge saddle. 

I don't know understand what you mean when you measure from the 1st fret to the... last fret on the fingerboard? I can't see how you get a scale length from what you seem to be doing. Can you draw me pictures or something?

[Frank Ford]

We generally state the scale length as the leading edge of nut to the middle of the 12th fret multiplied by two.

Compensated bridge position is a separate issue and has some variables - stringing, tuning, action, etc.  That we derive by experiment, experience, or calculation, like this:  Calculating Intonation Correction

We notice surprisingly wide discrepancies between measured scale length and that specified by lots of manufacturers, and 1/8" or so is no issue for me. . .

[Robbie Collins]

Thanks for weighing in, Frank. I'll check out that article.

I watched some machine shop videos tonight put out by the engineering department at MIT and thought about your articles on machining:

http://techtv.mit.edu/videos/142-machine-shop-1

I learned a lot - layout with blueing, transfer punches & screws, drilling accurate holes, etc. A Wilton drill press...wow.

[David Farmer]

Sorry, I was not trying to confuse.

With a fret table and some subtraction I figure the distance from the 1st fret to the 21st  should be 16.488" for the 25.5 scale and 16.405" for the 25.375". that's a difference of over a 16th and visible on a carpenters tape.

It's a way of figuring out what scale length was used to lay out the frets,  independent of the bridge and fret board end.

I find this method sometimes gives me another useful piece of information when I am trying to figure out what is going on.

Hope that's more helpful.

[Ned Knepp]

Thanks, David, now I understand what you are doing.

[David Collins]

Though it's a bit late to get in to it, I'll actually be doing a presentation on this at the Northwoods seminar in a few weeks. 

For a brief overview, here's something I wrote up a few years ago - bear with me in my long winded explanations...

------

Though it may seem a basic and fundamental point of fretted instrument design, “scale length” has become (or perhaps always been) a rather ambiguous term in the field of fretted instruments. There are in fact several distinct definitions applied to the term by different companies and technicians, as well as some common usages which I hesitate to qualify as proper definitions. The Martin Guitar Company’s use of the term is a prime example of this*.

At least for the purpose of this writing, I will clarify my own definitions of two distinct descriptions of scale length that are most commonly used.

Base Scale Length: The base number from which the fret spacing is calculated. In other words, it is the original length from which the fret scale (i.e., rule, template) is laid out.

Relative Scale Length: 2x the distance from the nut to the center of the 12th fret. This definition does not always directly determine or reflect the spacing of the frets relative to each other. Though this is probably less pure a definition of scale length than the former, it is generally considered the more useful of the two, and certainly more widely used. Its value lies both in its ease of calculation, as well as its ability to provide consistent comparisons between boards of different fret placement systems. Assuming all setup criteria remain constant between them, and intonation is conventionally adjusted to 0¢ offset at the 12th fret, the same relative scale length will result in the same end string length, even between boards of different fret spacing systems or nut compensation.

*In efforts of disambiguation, at least one other common use of the term deserves to be mentioned. The Martin Guitar Company defines their “scale length” according to the open length of the high E string, including average compensation (of approximately .060”). This method of defining scale length as the total length of a string is likely carried over from non-fretted relatives such as the violin. On fretless instruments where there are no frets to govern the total string length, the string length of course will instead dictate the fingering positions. This makes defining scale length as the total string length both appropriate and necessary as a relative term for comparing these instruments.

On fretted instruments however, I feel this usage suffers great inadequacies. Foremost is the fact that with a system of straight frets, each string will require a different amount of compensation, and end at a total open length different from others. This leaves the rather arbitrary choice of which string or point along the saddle one chooses to refer to. Martin uses the total high E string length today, but you will hear of others using the average among all strings, and still others choosing the low E. Furthermore, the end length with compensation will change relative to details such as setup or string choice, presenting us with the possibility of the same instrument being describable as several different scale lengths dependant on changes in these details.

While it is unlikely we will see this usage of the term disappear, I feel it best reserved for use as a layman’s approximation. It carries little to no benefit in any technical discussion, and can serve simply to confuse when any need for accuracy is involved. I have personally encountered cases in which small builders have misplaced their bridge, where the fingerboard was sold as a “25.4” scale, and the saddle template labeled the same, but the two used incompatible definitions. For purpose of technical discussions therefore, I prefer to omit this usage entirely, and reserve the term “scale length” to either the “relative” or “base” definitions listed above.

.....

If a board were slotted to the modern standard of 2^(1/12) spacing and the nut located accordingly with no compensation, the Base and Relative scale lengths would be identical. When a board is spaced to an alternate system such as the true rule of 18 however, the relative scale lengths would indeed be quite different, even though they began with the same base scale length.

For example, if a spacing were to start from a 24.75” Base Scale Length, and used the true rule of 18, the 12th fret would not fall at the halfway point of 12.375” as it would using the 2^(1/12) rule. Rather, it would fall notably short at 12.285”, and in order to intonate properly at the 12th fret, the bridge position would need to be adjusted accordingly. The same 24.75” Base Scale Length is used in each scenario, yet the Relative Scale Length of the “rule of 18” board would end up at 24.57”, while a 2^(1/12) spaced board's relative scale would remain at 24.75”. This is in fact where much confusion occurs in the labeling of scale lengths on Gibson guitars, and demonstrates the need to distinguish the two definitions as independent.

-------------

Epiphone originally used the more modern 12th root of 2 spacing, but when they were acquired and manufactured by Gibson their instruments of course assumed Gibson methods, which was (and still is on most of their instruments) spaced to the literal rule of 18. This means that if they were making a 25.5" base scale board, by using an even 18 divisor they would end up roughly at 25.315 relative scale (12.657"-ish nut to 12th). In the 60's however, Gibson-made boards tended to lean on the long side most likely due to tooling errors in spacing or blade thicknesses. Their nut edge of the board is also typically inconsistent with the fret spacing (can be either long or short), but most would probably measure out in the range of 25.32"-25.36" relative scale. 

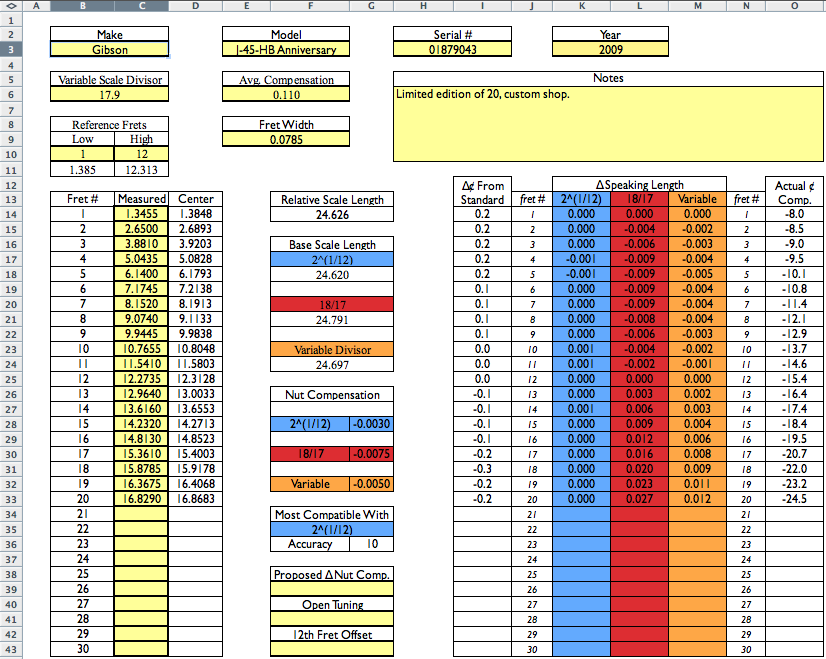
As to how to measure, my methods and tools are probably a bit complicated for most. I use customized calipers like these - 

and a spreadsheet like this - 

... which allows me to enter each fret, select variable reference frets to gauge by, and view additional charts and graphs to project final effects on intonation. 

Back from the world of theory and to your specific case though, at some point you have to accept some of the quirks and be pragmatic. Yes, there are ways to factor in all this data to make more detailed judgements on how to shuffle around the inconsistencies to minimize their noticeability, but that can get a bit more complicated (which is why I won't have any problem filling a 4 hour lecture on this topic at Northwoods). Still, I know these 60's Gibson boards well enough to say that you should probably do just fine by measuring the nut to 12th and doubling it for your relative scale, and adding typical compensation to that.

I hesitate to recommend specific final measurements because I don't have your specific scale and your specific eyes (rounded measured numbers can be vary significantly with these factors), plus Gibson boards did vary quite a bit in this era. If there's one thing to take from what I've put forward here though, it's that you should not be tempted to assume whole, round, logical numbers. If your nut to 12th measures 12.67", then it's 12.67", or 25.34 relative scale (not 25_5/16 or 25_3/8"). Resist the urge to round to fractions semi-rational numbers because you assume there is some sensible intentions behind the lengths. Sometimes by the time you figure in the mathematical oddities and tooling errors, there just aren't, and you have to play the ball from where it actually lies. 

By the way - Frank, I'm sorry you can't make it out to the Northwoods revival this year. Certainly won't be quite the same without you there. 

[Robbie Collins]

Brilliant! Thanks for going to the trouble, David. This is exactly what I've been missing in my understanding.  I've been edified! I'm going to print this out, reread, and research this a little more.

I hear you about the temptation to round. While my eyes were reading 11/32 my brain kept rooting for 5/16, thinking my eyes were suffering a parallax view.

I wish I could go to Michigan...that would be bee's knees! I bet it's beautiful up by the National Forest. I imagine that the disappointment would be not being able to attend all sessions simultaneously. A 1000 dollars and a 1000 miles (sigh)...one day!